Epidemiological tag

A game

Shall we play a game?

• Each tagged player tags two others

• But only the first time tagged counts

• The game stops when the tagging stops

Let’s play with 31 players

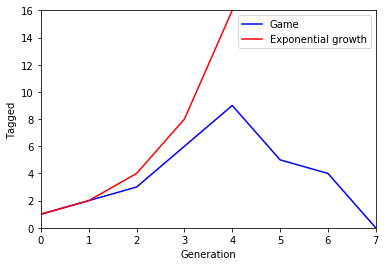
1 player tags 2 who tag 4 who tag 6 ≠ 8 at which point the game diverges away from exponential growth. The 6 players tag 7 who tag 4 who tag 3 who tag 0 and the game ends. Summing the generations results in 1 -> 3 -> 7 -> 13 -> 20 -> 24 -> 27 ≠ 31, so there is herd immunity for 4 players.

Let’s play again

1 player tags 2 who tag 3 ≠ 4 at which point the game diverges away from exponential growth. The 3 players tag 6 who tag 9 who tag 5 who tag 4 who tag 0 and the game ends. Summing the generations results in 1 -> 3 -> 6 -> 12 -> 21 -> 26 -> 30 ≠ 31, so there is herd immunity for 1 player.

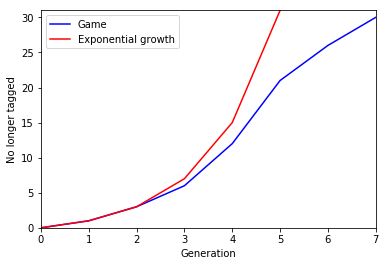
Let’s average 100 games of 1023 players

Results in the classic wave of infections. Summing the wave results in a classic sigmoid (S curve) showing herd immunity.

The reproduction rate

The reproduction rate (R number) is the number of people one person infects. Crunching the numbers results in the formula

S is the number of untagged players and N is the total number of players. For the tag game the initial R number, R0, is 2. The value of alpha may be read from the graph

If alpha were zero then the reproduction rate is constant and exponential growth is observed. If alpha were one then the standard model of Kermack-McKendrick (1927) results. Hence the tag game is less aggressive than exponential growth but more aggressive than the standard model.

Supporting material

The Tag subdirectory of the Github repository