How epidemics really grow
Everyone knows how an epidemic grows? One person infects two, those two infect four and so on. Alternatively the two try to infect each other and the first person thus the epidemic ends, or maybe something in between? An epidemic is a random process which contains non-random processes such as exponential growth with associated probabilities.
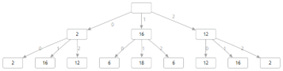
For a total population of seven where each of two infected people tries to infect two others and one immune person we can compute all the combinations of who tries to infect who and create a discrete probability distribution for the number of infected in the next generation.
900 P(0) = 2 × 2 = 4
900 P(1) = 2 × 16 + 16 × 6 = 128
900 P(2) = 2 × 12 + 16 × 18 + 12 × 12 = 456
900 P(3) = 16 × 6 + 12 × 16 = 288
900 P(4) = 12 × 2 = 24
The formula for the probability of exponential growth is such that for only one person infected in a population with no immunity then exponential growth is a certainty. As more people become infected this reduces until, when everyone has been infected, the probability becomes an impossibility as expected.
By increasing the numbers it is possible to approximate a continuous probability distribution. e.g. a population of 260 with 50 infected, 100 recovered and each infected person tries to infect two others results in a discrete distribution that is fitted by a logit-normal distribution.
Note that the logit-normal distribution is divergent at the start of an epidemic since the probability of exponential growth is always an impossibility. The average of the logit-normal distribution corresponds to the growth term in the Kermack-McKendrick model of 1927 - this model is the basis for many influenza and Covid-19 simulations.
Further reading
Epidemiological tag I: Derivation of the Kermack-McKendrick model. https://osf.io/sd8xz
Epidemiological tag II: The logit-normal growth of an epidemic. https://osf.io/s7fa8/