There are two types of people who believe epidemics grow exponentially; those who failed Maths and those who copied other people's homework. Unfortunately the latter would seem to include celebrity Mathematicians such as Prof Marcus du Sautoy. In the following paragraphs I'll seek to explain exponential growth and epidemiological modelling to the reader. The basic arguments will be accessible to those with a secondary school education although some of the subtleties that I will seek to impart will require a knowledge of differential calculus.
Exponential growth
The exponential function is part of pure Mathematics. The reader will remember this branch of Maths from school and that their answers were only ever right or wrong. In contrast Mathematical modelling concerns answers that are always wrong, it just being a question of how wrong. To any competent modeller exponential growth is always suspect as, in the words of Buzz Lightyear, it goes to infinity and beyond.
Exponential growth occurs when at each step the quantity doubles (note that the step size can be adjusted to ensure the doubling). For example you have 2 parents, 4 grandparents and so on. The example given should be familiar to reader from its unthinking repetition in the media over the last few years. I say unthinking because it can be extrapolated back into the mists of time until you have more ancestors than people who have ever lived. This trolling of ideas is known as Reductio ad Absurdum, the particular law of Mathematics being broken is called realizability. Realizability is the acknowledgement of a finite world whereas exponential growth, were it to occur, requires infinite resource.
Epidemiological models
The exponential function is deterministic. i.e. for any given input value the output value is known. Epidemiological models are divided into two types. The first is discrete and stochastic; discrete meaning they apply to individuals, stochastic meaning the output is subject to chance. The second type is continuous and deterministic; continuous meaning an individual can be chopped up into parts smaller than atoms. Given the assumption that all individuals are equal, running a model of the first type multiple times and averaging should result in a model of the second type.
The continuous deterministic models are represented by a set of differential equations with respect to time, one of which is
I' = gamma (R - 1) I
where I is the number of infected people, gamma is the reciprocal of the amount of time a person is infected on average and R is the number of people a person will infect. If R is a constant and greater than one then exponential growth occurs. That R is never constant has been known since at least 1927 and the publication of the model of Kermack and McKendrick for which
R = R0 S / N
where R0 is a constant (the initial value of R) and S / N is the never increasing ratio of people who have never been infected to the total number of people. i.e. it models sub-exponential growth.
Some have argued that an epidemic grows exponentially then doesn't. For the continuous model that would mean that for some derivative of I there is a discontinuity at some time. i.e. Some event happens to change the value of R. This then has to be introduced in a manner that is not utterly contrived.
Why assume exponential growth?
Exponential growth appears to be assumed because it is easier to fit a straight line to a log plot of the number of infected than an actual epidemiological model. e.g. for a log-plot of Kermack and McKendrick it is easy to fit a straight line to the initial part of the curve, however knowing when to stop is hard.
This is somewhat borne out in a paper by seven authors from the Universities of Leeds, Southampton, Glasgow and the London School of Tropical Medicine that was subject to derision when it was announced on Twitter. In the paper the authors admit that they assumed exponential growth rather than fit a standard epidemiological model because the latter was too hard...


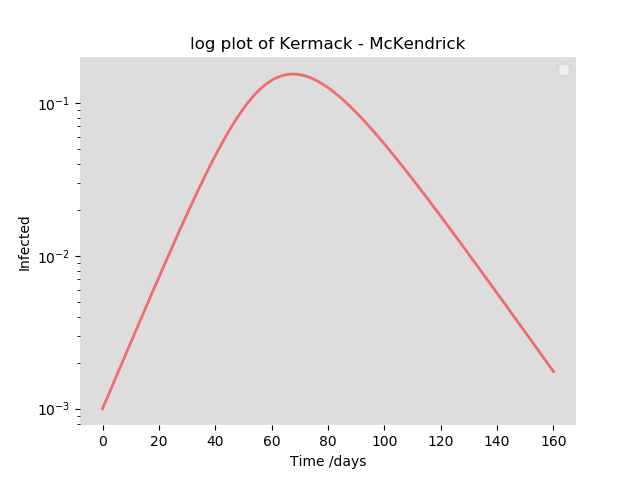
Indeed, when left to their own devices, epidemics always follow a Gompertz curve. Even before herd immunity is reached, the virus ultimately trips on itself and the wave crashes of its own weight.